Math Insight

There are two ways to take the product of a pair of vectors. One of these methods of multiplication is the cross product, which is the subject of this page. The other multiplication is the dot product, which we discuss on another page.

  1. $\vc \times \vc$ is a vector that is perpendicular to both $\vc$ and $\vc$.
  2. The magnitude (or length) of the vector $\vc \times \vc$, written as $\|\vc \times \vc\|$, is the area of the parallelogram spanned by $\vc$ and $\vc$ (i.e. the parallelogram whose adjacent sides are the vectors $\vc$ and $\vc$, as shown in below figure).
  3. The direction of $\vc \times \vc$ is determined by the right-hand rule. (This means that if we curl the fingers of the right hand from $\vc$ to $\vc$, then the thumb points in the direction of $\vc \times \vc$.)

This formula shows that the magnitude of the cross product is largest when $\vc$ and $\vc$ are perpendicular. On the other hand, if $\vc$ and $\vc$ are parallel or if either vector is the zero vector, then the cross product is the zero vector. (It is a good thing that we get the zero vector in these cases so that the above definition still makes sense. If the vectors are parallel or one vector is the zero vector, then there is not a unique line perpendicular to both $\vc$ and $\vc$. But since there is only one vector of zero length, the definition still uniquely determines the cross product.)

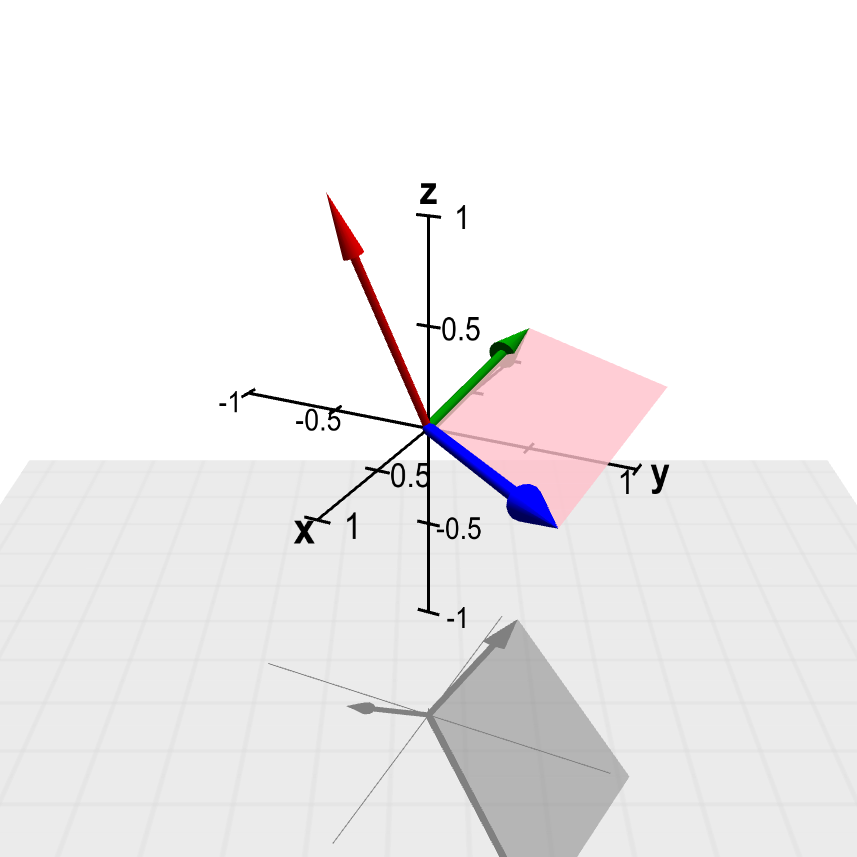
Below is an applet that helps illustrate how the cross product works. Although it is admittedly hard to manipulate in a precise manner, you can convince yourself that the above properties of the cross product are satisfied by the cross product vector shown in the applet.

Applet: Cross product

Applet loading

The geometric definition of the cross product is nice for understanding its properties. However, it's not too convenient for numerically calculating the cross product of vectors given in terms of their coordinates. For such calculations, you may want to have the formula for the cross product in terms of components. With the cross product formula in hand, you can make short work of any calculation, as illustrated by these examples of calculating cross products and areas of parallelograms.

Thread navigation

Vector algebra
Math 2374